Biggs–Smith graph
| Biggs–Smith graph | |
|---|---|
The Biggs–Smith graph |
|
| Vertices | 102 |
| Edges | 153 |
| Radius | 7 |
| Diameter | 7 |
| Girth | 9 |
| Automorphisms | 2448 (PSL(2,17)) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Symmetric Distance-regular Cubic Hamiltonian |
In the mathematical field of graph theory, the Biggs–Smith graph is a 3-regular graph with 102 vertices and 153 edges.[1]
It has chromatic number 3, chromatic index 3, radius 7, diameter 7 and girth 9. It is also a 3-vertex-connected graph and a 3-edge-connected graph.
All the cubic distance-regular graphs are known.[2] The Biggs–Smith graph is one of the 13 such graphs.
Algebraic properties
The automorphism group of the Biggs–Smith graph is a group of order 2448[3] isomorphic to the projective special linear group PSL(2,17). It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Biggs–Smith graph is a symmetric graph. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Biggs-Smith graph, referenced as F102A, is the only cubic symmetric graph on 102 vertices.[4]
The Biggs–Smith graph is also uniquely determined by the its graph spectrum, the set of graph eigenvalues of its adjacency matrix.[5]
The characteristic polynomial of the Biggs–Smith graph is : 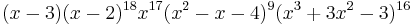 .
.
Gallery
References
- ^ Weisstein, Eric W., "Biggs–Smith Graph" from MathWorld.
- ^ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.
- ^ Royle, G. F102A data
- ^ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41–63, 2002.
- ^ E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189–202, 2003
- On trivalent graphs, NL Biggs, DH Smith - Bulletin of the London Mathematical Society, 3 (1971) 155-158.